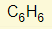0.
Formula of simple compounds
To figure out the chemical formula of a given compound all you need to know are the valencies of the atoms that make the compound.
The valency is the amount of electrons an atom has to gain or lose in order to achieve a full outer shell.
You can figure out the valency of an atom via the periodic table.

The group of the element (on the periodic table) tells you how many electrons there are in the atom’s outer shell. From this information, you can figure out how many electrons it needs to gain or lose to achieve a full outer shell. Groups 1-3 (metals) will LOSE electrons. Groups 5-7 (non-metals) will GAIN electrons. Group 4 can do either.
Also remember, many atoms will become ions due to the loss or gain of electrons in ionic bonding. This means the valency of an atom will also tell you the charge of its respective ion (i.e. Sodium ion = +1 charge. Chloride ion = -1 charge etc.)
So once you know the valencies of the atoms, all you need to do is swap the numbers around and cancel them out if they are equal. Take a look at the examples below, you will understand what I mean:
Examples
- What is the formula for Magnesium Chloride?
- Mg (valency 2) + Chlorine (valency 1)
- Swap the two numbers around
- Formula is therefore
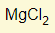
- What is the formula for Aluminium Oxide?
- Al (valency 3) + Oxygen (valency 2)
- Swap the two numbers around
- Formula is therefore
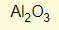
- What is the formula for Calcium Oxide?
- Ca (valency 2) + Oxygen (valency 2)
- In this case, because the valencies are equal, you must cancel them out
- Formula is therefore just CaO
Writing equations
This skill will be briefly introduced here and developed further throughout the course. All chemical reactions can be represented by equations. You need to know how to write both word equations and symbol equations.
Word equation
These are very simple. You simply write the equation in words. For example:
Magnesium + Oxygen -> Magnesium Oxide
Symbol equations
This is the most common type. Atoms and compounds are represented by their symbols. This is a bit more complex because the equation needs to balance.
A balanced equation means that there are the same number of each type of atom on both sides of the chemical equation. For example:
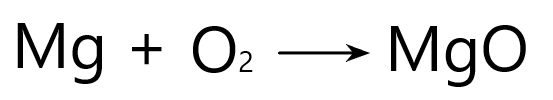
As we learnt above, we know that the chemical formula for magnesium oxide is MgO because magnesium and oxygen both have a valency of 2 which cancels out.
Now if you look closely, the above equation is not balanced. Why? Because the left hand side has two oxygen atoms, but the right hand side only has one.
At this point you may ask. Why can’t the oxygen just be written as a single O instead of O2? Then that would solve the issue. Unfortunately it doesn’t work that way because some elements will always be found in molecules (i.e. two atoms bonded together). Oxygen, nitrogen, chlorine, and hydrogen are all examples of this.
Then can we change the formula of magnesium oxide into MgO2 to balance the equation? No. We can’t do that. We know that the formula is MgO. You can not change the original chemical formula of a compound.
So how the hell do we balance this thing? Well, we do so by adding numbers in front of the reactant or products like so:
![]()
Now if you look at it, the equation is balanced!
- LHS = 2 Mg and 2 O
- RHS = 2 Mg and 2 O
State symbols
State symbols represent the physical state in which the reactions or products are in a chemical reaction. For example:
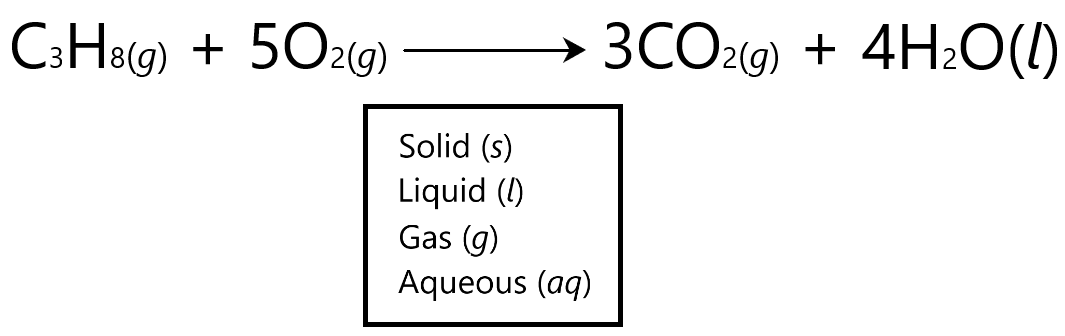
Calculations
Definitions

Mole equations
Many of the calculations that you’ll need to do will involve the concept of moles. There are three important equations that you need to learn:
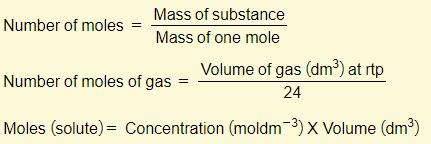
You must memorize these three equations off by heart and also have the ability to rearrange them. A lot of the calculation examples below will make use of these equations so you must be comfortable with these.
Moles and masses
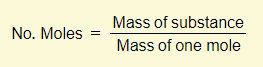
Example 1 – Calculate the relative formula mass of the following: (You can use the periodic table)
Remember, the relative formula mass (Mr) is just a sum of all the different relative atomic masses (Ar). The Ar is really just a fancier term for “mass number” and this can easily be found in the periodic table!
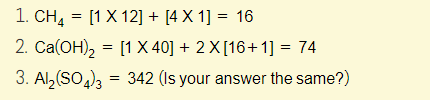
Example 2 – Calculate the mass of one mole of the following:
Remember, one mole is equivalent to 6X10^23 atoms, molecules or ions of the substance. The mass of one mole of a substance is equal to the relative formula mass (Mr)!
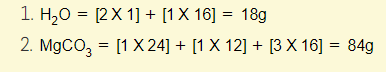
Example 3 – Calculate the mass of each of the following:
Now that you know the mass of one mole of any compound is equal to the relative formula mass, you can calculate the mass of a given compound as long as you know how many moles there are!
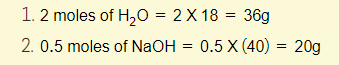
Example 4 – Calculate the mass of magnesium oxide formed when 3.0g of magnesium reacts with excess oxygen
* Step 1: Write down a balanced chemical equation
* Step 2: Calculate the amount of moles of the reactant
* Step 3: Calculate the amount of moles of the product
* Step 4: Calculate the mass of product
Firstly, write down a balanced equation:
![]()
- 3.0g of Mg = 3/24 = 0.125 moles (of Mg)
- The mole ratio between Mg and MgO is 2:2 (or 1:1). Therefore, 0.125 moles of Mg will form 0.125 moles of MgO.
*The mole ratio is the ratio of ‘big numbers’ in front of the reactants and products inside the equation. In this case, Mg and MgO both have a number 2 at the front. Therefore the ratio is 2:2 (and thus 1:1). In this scenario, one mole of Mg will form one mole of MgO. Theoretically, if the ratio was 1:2 that would mean one mole of Mg would make 2 moles of MgO.
- Since 0.125 moles of MgO is formed, the mass can be calculated via mole equation 1
- 0.125 X (24+16) = 5.0g of MgO has been produced from 3g of Mg in excess oxygen.
Moles and volumes
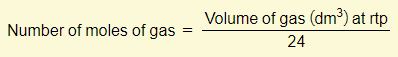
Example 1 – Calculate the amount of moles of oxygen molecules in the following volumes of oxygen at rtp:
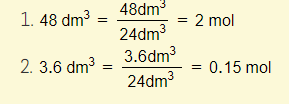
Example 2 – Calculate the amount of volume of oxygen at rtp for each of the following masses of gas:
Do not be confused. This is simple! First figure out the number of moles of oxygen (mass/Mr). Now simply apply mole equation 2 and you’re done!
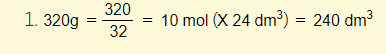
Example 3 – Calculate the volume of oxygen at rtp required to burn 1.4g of butene:
The balanced chemical equation will most likely be provided:
![]()
*The way you approach this question is very similar to example 4 from ‘reacting masses’ above. To calculate the volume of oxygen required, all you need to know is the moles of oxygen that is required. We know that the mole ratio of butene to oxygen is 1:6 so that means for every mole of butene, 6 moles of oxygen is required. All we need to know, then, is the amount of moles in 1.4g of butene and that is easy!
- 1.4g of butene = 1.4 / (4X12 + 1X8) = 0.0259 moles
- 0.0259 moles of butene requires (0.025 X 6) moles of Oxygen due to 1:6 mole ratio. This equates to 0.15 moles (of oxygen)
- 0.15 X 24 = 3.6
 is the volume of oxygen required
is the volume of oxygen required
Moles and concentrations
![]()
Example 1 – Calculate the volume of sodium hydroxide, concentration 0.16 mol/dm^3, needed to neutralize 20cm^3 of sulphuric acid, concentration 0.2 mol/dm^3
The balanced chemical equation is as follows:
![]()
*Using the mole equation above, start by calculating the amount of moles in sulphuric acid. The mole ratio here is 1:2, meaning for every mole of sulphuric acid, double the amount of sodium hydroxide will be required. Once you’ve figured out the required amount of moles of sodium hydroxide, the volume can easily be obtained by rearranging the formula.
*Also remember, cm^3 needs to be converted into dm^3 by dividing by 1000
- Moles (sulfuric acid) = 0.2 X (20/1000) = 0.004
- Moles (NaOH) = 0.004 X 2 = 0.008
- Volume (NaOH) = 0.008/0.16 = 0.05
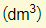
% Yield
In a chemical reaction, the expected/calculated amount of product is the theoretical yield. Unfortunately however, the product amount actually produced (actual yield) is often lower than this theoretical amount. Taking a ratio of these two values gives us the % yield.
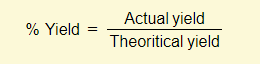
Example – Excess magnesium carbonate was added to 25cm^3 sulfuric acid, concentration of 2.0mol/dm^3. The unreacted magnesium carbonate was removed by filtration. The solution of magnesium sulfate was evaporated to give 6.7g of hydrated magnesium sulfate crystals. Calculate the percentage yield
Balanced chemical equation is as follows:

The question tells you that 6.7g of crystals were formed, so therefore this is the actual yield.
The theoretical yield can be calculated as follows:
- Moles (H2SO4) = 25/1000 X 2 = 0.05
- Moles (MgSO4.7H2O) = 0.05 (Because mole ratio is 1:1)
- Relative formula mass (MgSO4.7H2O) = 246
- Mass = 0.05 X 246 = 12.3g (theoretical yield)
- % yield = 6.7/12.3 = 0.545 (54.5%)
*The original answer is in decimals. To convert decimals to percentage, multiply by 100
% Purity
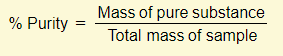
Example – 7.0g of impure calcium carbonate was heated and 2.42g of carbon dioxide was collected. Calculate the percentage purity of the calcium carbonate
Chemical equation:
![]()
The key thing here is that carbon dioxide can only be made from pure calcium carbonate. The impurities in the original sample (of 7.0g) will not contribute to the production of carbon dioxide.
The percentage purity can therefore be calculated as follows:
- Moles (CO2) = 2.42 / (12 + 32) = 0.055
- Moles (CaCO3) = 0.055 (Mole ratio 1:1)
- Relative formula mass (CaCO3) = 100
- Mass (Pure CaCO3) = 0.055 X 100 = 5.5g
- Percentage purity = 5.5/7 = 0.786 (78.6%)
Empirical and molecular formula
Example – A hydrocarbon contains 92.3% carbon and 7.7% hydrogen. It’s relative molecular mass is 78. Calculate it’s empirical and molecular formulae
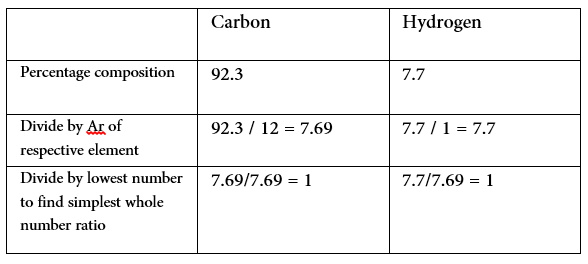
The ratio of carbon to hydrogen is therefore 1:1
-
- Empirical formula (simplest ratio) is therefore CH
- The molecular formula is a multiple of the empirical formula. The Mr of the hydrocarbon is 78 and the Mr of our empirical formula (CH) is 13, giving us a multiple of 6. The molecular formula is thus: